Why I like TikZ’s Math Library

I’m not a texpert. I’m a mathematician, that started programming on BASIC, then moved to C, C++, Java, PHP, Python and finally to JavaScript. Moving from one of this languages to another is easy, up to some syntactic sugar, it is time consuming but not so hard. I have never been able, nor attracted, to be honest, to program on TeX.

And for this reason when I discovered the math library, introduced with TikZ 3.0 almost a year ago, that allows us to use a syntax close to ordinary programming languages, I was so excited.

Let’s start by one example to see how it works.

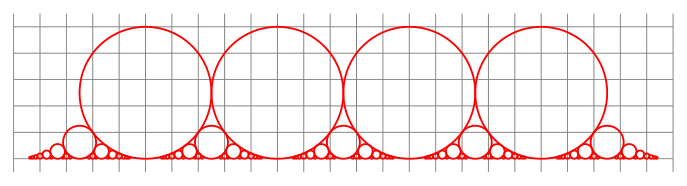
The Ford circles

Given an irreducible (very important) fraction $\frac{p}{q}$, we place a circle at $(\frac{p}{q},\frac{1}{2q^{2}})$ with radius $r = \frac{1}{2q^{2}}$. This circle is tangent to the abscissa. And if we put all this circles, they do not intersect, and some of them are tangent.
For more information you can check Ford circles on Wikipedia.

The questions is : Given an interval $[a,b]$ and a number $n$, how to draw all Ford circles for simple fractions $\frac{p}{q} \in [a,b]$ such that $0 < q < n$ ?

To do this, we can use math library to create a function FordCircles(\a,\b,\n) that do the job. And then simply call this function inside tikz picture environment with something like \tikzmath{FordCircles(-.9,3.9,8);}.

Here is the code and the result :

Let’s do some comments on the code :

Line 4 :

We enter in the world of tikzmath.

Things to know :

• ALL instructions end with semicolon;
• in some places space are ignored, in other places they are not and can generate errors (check the comment for line 7).

Line 5 :

We declare our function. A function can take more then 1 parameter. The documentation says that we can have a function without parameters and in this case we can omit the parentheses, but I was not able to make this work. The parameters could be only numerical (numbers, lengths, counters), no strings, no points, no arrays.

Line 6 :

We announce that the variables \p and \q are integers. In this way if we assign a non integer value to one of them it is automatically converted with int() function. For example \p = 3.5; is the same as \p = int(3.5);.

Line 7 :

We can use for loop. It is not as powerful as \foreach from pgffor library, but the syntax is similar. Be careful, if you put a space between }{ this will generate error. This is because inside functions, spaces are not completely ignored.

Line 8 :

We can nest loops. You can notice that we were supposed here to use int(\a*\q) and int(\b*\q) to obtain integer limits for \p, but as we have declared \p as integer, all parameters in for are automatically truncated to integers.

Line 9 :

We can make decisions with if.

Lines 10-11 :

We create the macros \f and \r, that can be used later by the “outside world”, in particular by TikZ here. And, as we precompute these values, we don’t need the calc library.

Lines 12-14 :

We can output some text by putting it in curly brackets { };. For more details see the next section. And the variables \f and \r are available in the “outside world” as standard tex macros.

Lines 15-18 :

We can smash all this lines to win place, but this will reduce the readability of the code. And I think (and I’m not the only one) it’s a bad idea.

Exercice :

Try to modify the code in a way to fill the circles with color that varies between red and blue. And to print the value of $\frac{p}{q}$ inside it. The result should be something like this :

You can find the solution here.

How math library communicate with the outside world ?

Method 1

The math library is cleaver enough to modify existing macros, counters and dimens like any other variable. And if some variable do not exist, it creates it as a standard tex macro. So we can access it event outside tikzmath.

We can see this in the Ford Circles’ code with \f and \r that are created inside tikzmath and used outside by TikZ

Method 2

tikzmath can “print” text to the “outside world” with two different, but close commands :

• As on lines 12-14 in the Ford Circles example, we can “print” to tikz using curly brackets followed by semicolon.
• If we want to “print” in the standard TeX world (where font is not set to nullfont), it is better to prepend the curly brackets by the word print like this : print {the point $A_\i$};.

Method 3

A numerical function defined inside tikzmath can be used inside tikzpicture like all predefined functions.

For example we can define the cardinal sine function sinc such that $sinc(x)=\frac{sin(x)}{x}$ if $x \neq 0$ and $sinc(0) = 1$. And then use it like we use sin for example.

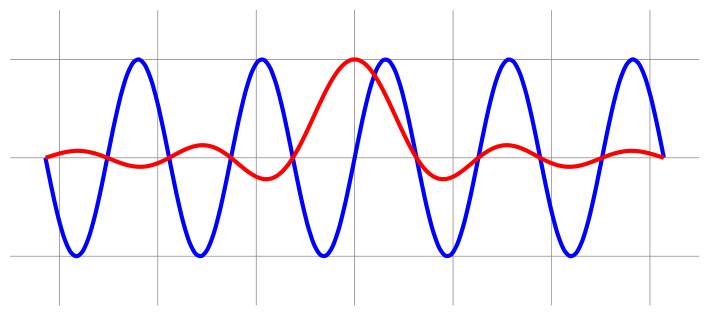
Note on return : In the manual we can read that the return should be the last executed line. This is not exactly true, but what you should know is that return does not stop the execution of the function (unlike in classical functional languages). So for readability reasons it is better to have no lines executed after.

Recursive calls

There is one more aspect that I would like to demonstrate you : the ability of recursive function calls. This feature can be very useful to draw racursives structures (such as fractals for example).

To illustrate this let’s draw a Cayley graph of a free group, that is a 4-regular tree. For this purpose we create a function Branch(\x,\y,\rotate,\step) that :

• draws one edge at position (\x,\y) with direction \rotate and size \power^\step (where \power is a fixed parameter),
• and then call itself to draw all three child edges (and their child edges).

Remark : The compilation time for 7 levels of recursion is more than 20 seconds. And we can’t do it for 8 levels because there is memory overflow.

What I regret ?

I like very much tikzmath, but as any first version of some software, there are things that can be improved.

• I regret that I was not able to create function without parameters. This is probably my personal mistake.
• I regret that we can’t create functions with non numerical parameters. For example if we want to create a function that takes two colors and return a mixture of this colors, we can’t do it for the moment.
• I regret the name of this TikZ library : math. This library is about functional programming and has nothing to do particular with math, except the limitation that the function parameters are necessarily numerical.